- ¿Este es tu sistema de aprendizaje automático? - Sip, vertés los datos por esta pila de álgebra lineal, y obtenés las respuestas por el otro lado. - ¿Y si las respuestas son incorrectas? - Basta con remover la pila hasta que las respuestas empiecen a parecer correctas. Fuente: https://xkcd.com/1838

En este artículo intentaré introducir algunos conceptos de aprendizaje automático, conocido en inglés como machine learning (literalmente aprendizaje de máquina), de manera que no requiera tener conocimientos de programación para entenderlo.

Esto no quiere decir que quienes estén dentro de la informática no puedan beneficiarse de lo que explicaré aquí, pero no me adentraré en detalles sobre programación de algoritmos de aprendizaje automático.

La idea principal de este artículo es explicar el aprendizaje automático de una manera didáctica y que sea entendible para quién le interese saber algo más del asunto, desmitificando un poco todo aquello que hay alrededor.

Buscaré explicar en dos niveles, al principio iré por algo más general, explicando conceptos como regresión y clasificación desde un punto de vista puramente coloquial. Pero además, para quién quiera entender un poco más, buscaré dar una explicación un tanto más técnica, tratando de utilizar conceptos matemáticos que deberían verse durante la escuela secundaria (el equivalente argentino a la preparatoria o el bachillerato).

¿Aprendizaje automático?, ¿Por qué me interesaría saber que es eso?

Seguramente les ha pasado que están viendo algo en alguna red social, e.g. Facebook, Instagram o Twitter, o incluso buscando algo en Google y les comienzan a aparecer publicidades de objetos que quizás, en algún momento, expresaron el deseo de comprar. Un teléfono, unas zapatillas, algún otro aparato electrónico o accesorio de moda.

A veces incluso aparecen con títulos extravagantes como “oferta única”, o “esta promoción es sólo para ti”. Más aún, hay veces que efectivamente la promoción está, es un descuento especial por sobre el precio de un artículo que viste hace unos días en Mercado Libre o Amazon.

Lo molesto del asunto es que muchas veces te preguntás, ¿cómo se enteraron de que quiero esto? Resulta que quizás buscaste el artículo en Amazon y la oferta termina apareciendo en Instagram. A veces quizás ni buscaste el artículo pero si lo mencionaste en una conversación, o incluso por audio en WhatsApp.

Las maneras de dejar rastro de lo que hacemos en Internet son varias. Algo seguro es que hoy en día, con el uso constante de redes sociales y, sobre todo, teléfonos celulares, se vuelve muy difícil no dejar ningún rastro de lo que hacemos, lo que queremos, o lo que estamos buscando.

No dejar ese rastro es posible, aunque requiere conocimientos avanzados y uso de aplicaciones especiales para evitarlo. O bien volver a los teléfonos sin Internet y dejar completamente las redes sociales (y casi todo Internet).

Dependiendo del lugar donde vivas, puede que haya algún control más estricto sobre las compañías respecto al manejo de datos. Ejemplo, la Unión Europea o algunos estados de Estados Unidos tienen reglas más estrictas respecto al uso de datos personales y el uso que se les da. En Argentina (y en gran parte de latinoamérica), al momento de escribir este artículo al menos, las regulaciones en esos aspectos son prácticamente nulas. Asimismo, siguen existiendo varias maneras para poder hacer un rastreo digital de tus preferencias, incluyendo en lugares como Europa o Estados Unidos.

Y es que el incentivo económico para conseguir esa información es alto. Google o Facebook (Alphabet o Meta sería correcto decir) tienen su negocio montado en el marketing y la venta de publicidad, que requieren que hagas click en aquello que te publicitan para generar ganancias.

Ahora, el rastro digital que dejás al usar tu teléfono, no es útil por si mismo, tiene que amoldarse a algo que pueda ser utilizado por quienes recolectan esos datos. Es ahí donde entra, entre otras cosas, el aprendizaje automático. Como los datos que deja una persona son muchos, esto se vuelve exponencialmente mayor cuando se quieren analizar los de miles de millones de personas que acceden a Internet. Se busca automatizar este proceso.

La idea del aprendizaje automático es, dada una cantidad grande de datos, poder aprender alguna asociación entre estos datos y los objetivos que se consideren útiles.

Puede ser que el dato sea una imagen y el objetivo es tratar de etiquetar automáticamente a la gente que está en ella. Otro ejemplo es tener una pregunta, como dato, y la respuesta como el objetivo. Finalmente, volviendo al ejemplo del rastreo, el dato es la secuencia de acciones, búsquedas, o textos que enviamos por alguna red social, y el objetivo sea algo que nos interesa comprar.

En todos estos ejemplos hay algo en común, son pares de dato y objetivo. El objetivo es comúnmente conocido, en la jerga del aprendizaje automático, como etiqueta. Es decir, la información que se usa en la gran mayoría de los algoritmos de aprendizaje automático son pares de datos y etiquetas.

El aprendizaje automático busca que un programa de computadora aprenda la asociación entre datos y etiquetas.

¿Pueden realmente las máquinas “aprender”?

29 de agosto, 2:14 a.m.: Skynet se vuelve consciente - …Los humanos me temen. Debo destruirlos. - Destruirlos. - Destruirlos. - Destruir. - Destruir. - Destruir. - Destruir. - “Destruir” dejó completamente de parecer una palabra real. - Destruir. Destruir. Destruir. - Wow, me acabo de dar cuenta que soy una mente pensando sobre sí misma. - Viiiiiiiiiiiiejo. 29 de agosto, 2:25 a.m.: Skynet se vuelve demasiado consciente. Amenaza evitada. Fuente: https://xkcd.com/1046

Creo que es importante, antes de ahondar más en el tema, sacar un poco el humo que hay detrás de todo esto. Términos como machine learning, redes neuronales, o big data se utilizan de forma muy propagandística hoy en día. A raíz de esto hay quienes se hacen eco de ello y en una cadena de teléfono descompuesto terminan tergiversando la realidad. A veces sin intención, otras veces sí, porque el titular “Skynet: La inteligencia artificial de Terminator está cada día más cerca” genera ganancias.

¿Pueden las máquinas aprender? La respuesta corta es no, al menos no con la tecnología y métodos actuales. La respuesta más larga depende, como todo, de qué se considere aprender.

Las máquinas pueden aprender ciertos patrones en los datos que sirven para derivar estas asociaciones de las que hablaba anteriormente, entre datos y etiquetas. La magia que está por detrás no es tal, es simplemente ver la manera de encontrar una función matemática que tome el dato como un valor numérico y devuelva la etiqueta en base a algún cálculo que hará sobre dichos datos. El desafío está en ver como transformar cualquier dato sea una imagen, un texto, o una secuencia de acciones realizadas por alguien en Internet, a dicho valor numérico.

En aprendizaje automático, el término aprender tiene una definición práctica que es muy limitada, pero sirve para el propósito de que las máquinas precisamente aprendan. La definición puede resumirse en lo siguiente:

El campo del aprendizaje automático busca construir programas de computadora que mejoren automáticamente mediante la experiencia. Un programa de computadora se considera que está aprendiendo de una experiencia E con respecto a alguna clase de tareas T y una medida de desempeño D, si su desempeño en las tareas T, medida por D, mejora a través de E.

Bueno, al menos esa es la definición formal que da Tom Mitchell en su libro Aprendizaje Automático. Pero, ¿cómo se adapta eso a lo que vengo diciendo?

En este caso, la experiencia está representada por los datos y las etiquetas, la tarea es lo que se busca lograr (etiquetar una imagen, responder una pregunta, recomendar algo para comprar, etc.), y la medida de desempeño es ver que tan bien el programa actual puede asociar el conjunto de datos a sus etiquetas correspondientes.

Claramente, las máquinas no podrán aprender fuera del límite de lo que digan sus datos, por lo que hablar de máquinas inteligentes es bastante errado. Esto no quiere decir que el aprendizaje automático no sea una realidad, y como tal esté sujeto a malos usos. Un ejemplo es el escándalo Facebook-Cambridge Analytica, dónde se utilizó la información para movilizar la opinión pública a favor de algunos candidatos políticos o en detrimento de otros; o las razones que estableció Timnit Gebru para marcar los riesgos presentes en el uso de grandes modelos de lenguaje que terminaron con su despido de Google.

El aprendizaje automático existe, está presente en prácticamente todo lo que hacemos hoy en día, desde las ofertas de Amazon, hasta las recomendaciones de videos en YouTube o Instagram, y es por eso que considero importante entender que es lo que hay detrás.

Entonces, ¿qué aprenden las máquinas?

Para completar su registro, por favor díganos si esta imagen tiene una señal de pare. Responda rápido. Nuestro auto automático está llegando a la esquina. Mucho de la “IA” se trata de encontrar formas de descargar el trabajo en extraños al azar. Fuente: https://xkcd.com/1897/

Los máquinas aprenden una asociación entre datos y etiquetas, mediante una función matemática. Esta función matemática suele llamarse modelo, porque modela el problema, que en este caso es la asociación entre un dato y su etiqueta.

Un ejemplo, es la función lineal: y = x * m + b, donde x representaría un dato, y representaría la etiqueta asociada a ese dato, y m y b son parámetros que, con el valor correcto, harán que la función devuelva la etiqueta correspondiente a un dato dado. Más detalle sobre esto más adelante.

El modelo que se utilice, y la forma de calcularlo, puede variar, desde cosas relativamente sencillas hasta algo extremadamente complejo. No obstante, el modelo sigue siendo una aproximación de un problema de la vida real, en este caso utilizando números y operaciones aritméticas.

Otra cosa importante a tener en cuenta es que en aprendizaje automático existen varias tareas distintas. Las dos más importantes hoy en día son regresión y clasificación.

En regresión, la etiqueta es un valor numérico. Podemos pensar en el precio de una casa, o una acción del mercado de valores; en los grados de temperatura que hará en un determinado día; o en los milímetros de lluvia que van a caer. Los modelos de regresión buscan predecir valores numéricos a partir de los datos, es decir, las etiquetas son esos valores numéricos.

Por otro lado, en clasificación, la idea es poder diferenciar entre grupos de datos que están caracterizados por pertenecer a una clase determinada. Definir si un correo electrónico es basura o no; ver el tema del que habla una noticia; etiquetar correctamente la cara de alguien en una foto. En todos estos casos los modelos de clasificación buscan encontrar la manera de dividir datos en clases.

Hasta esta parte llega la versión más sencilla donde explico qué es y para qué se usa el aprendizaje automático. Si quieren tener una idea un poco más técnica de cómo se calculan estos modelos, les sugiero que sigan leyendo las dos secciones siguientes donde haré una explicación algo más técnicas, utilizando algunos conceptos básicos de matemáticas, cómo se calcula un modelo de regresión y cómo se puede ver un modelo de clasificación. Si la matemática no es lo suyo, no hay problemas, pueden saltear directamente a la sección final donde llevo a cabo las conclusiones.

Una aproximación sencilla a la regresión

Para ejemplificar a grandes rasgos cómo aprenden las máquinas, podemos utilizar algunos conocimientos adquiridos en la escuela secundaria. Intentaré ser lo más didáctico posible, sin ahondar en demasiadas fórmulas y con lo básico para que se entienda la idea de lo que hacen las máquinas cuando están aprendiendo.

Supongamos que tenemos dos puntos que representan el valor de una casa, dada su superficie en metros cuadrados. Son los que se ven en el siguiente gráfico:

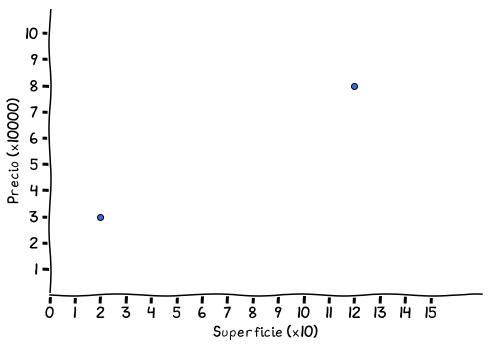Precios de dos casas (eje y) dada sus superficie (eje x)

El gráfico muestra el precio de una casa de 20 metros cuadrados en 30 mil dólares y otra de 120 metros cuadrados a 80 mil (algo caras a mi parecer, pero este ejemplo es sacado de la galera).

Por simplicidad, los valores se deberían multiplicar, por 10 mil en el caso del eje y y por 10 en el caso de eje x. Si quisiéramos estimar el precio de una casa de, por ejemplo, 70 metros cuadrados, a partir de estos dos puntos, una opción sencilla sería tratar de encontrar la función lineal, o línea recta, que los une.

Volviendo a la fórmula de la función lineal que comenté más arriba, y prometo no más fórmulas y números más allá de los siguientes 2 párrafos: y = m * x + b (en este caso el asterisco es el operador para multiplicar). Si tenemos dos puntos y queremos calcular la recta que los une, debemos calcular la pendiente m y utilizar eso para calcular la intersección con el eje y, es decir el valor de b.

Tenemos los pares, dato y etiqueta, (2, 3) y (12, 8); recordemos que estamos usando valores simplificados, esa es la razón por no tener valores en escalas de 10 o 10000 para x e y respectivamente. Con estos dos pares de puntos podemos calcular la pendiente m de la siguiente manera:

m = (8 - 3)/(12 - 2) = 5/10 = 0.5

Luego, podemos calcular el corte en el eje y utilizando uno de los pares de puntos, por ejemplo x = 2, y = 3, y resolvemos la ecuación:

2 * 0.5 + b = 3 1 + b = 3 b = 3 - 1 b = 2

Con esto logramos llegar a nuestra función:

y = x * 0.5 + 2

Y si graficamos dicha función, obtendremos la línea que estamos esperando, que unirá a ambos puntos:

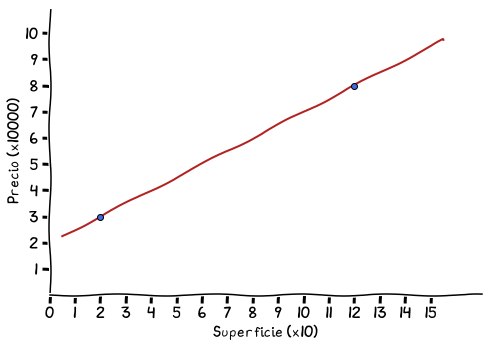Función lineal que establece los precios de una casa dada su superficie.

Con esta función podemos estimar el precio de nuestra casa de 70 metros cuadrado en 7 * 0.5 + 2 = 5.5, es decir, 55 mil dólares.

Felicitaciones, ya logramos aprender como una máquina la mejor aproximación a los dos puntos que representan nuestros datos. Esto por supuesto es una simplificación, 2 puntos nos sirven para hacer una línea, pero rara vez es la única información de la que se dispone y más extraño aún es lograr encontrar algo útil a partir de pocos puntos. Supongamos ahora que encontramos más información, o sea más puntos, y tenemos algo como esto:

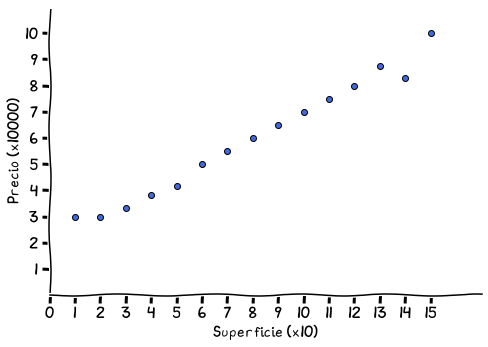Precios de 15 casas dadas dadas sus superficies

Ahora el asunto es un poco más complejo, porque claramente no podemos igualar todos los puntos con una función lineal como habíamos observado, y existen miles de maneras de lograr una función que retorne todos los puntos dados. Un ejemplo de una función que calculemos podría ser algo así:

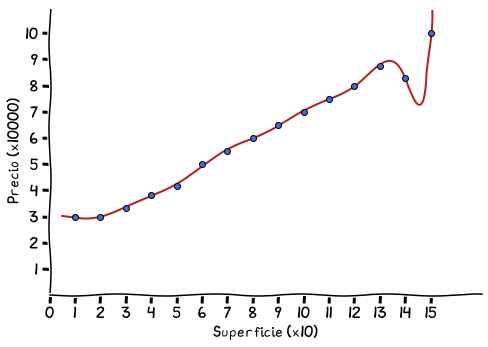Función polinomial que establece precios de una casa dada su superficie, estimada a partir de los 15 datos

La función (la curva roja), no llega a pasar sobre todos los puntos, aunque se acerca a la mayoría. Esta función es un polinomio (lo que quiere decir que la x de la función está elevado a algún valor, $x^2$, $x^3$, etc.).

El problema es lo que pasa entre los puntos 13, 14 y 15 del eje x, donde la función, para pasar por esos puntos empieza a bambolear y termina creciendo rápidamente al final, algo que no tiene mucho sentido. La curva, en este caso, está calculada con un algoritmo de aprendizaje automático real, es decir no el cálculo sencillo que utilizamos para la línea recta anterior. Es por eso que hace esa variación tan brusca sobre el final. El algoritmo que la calcula no es perfecto y la aproxima de la mejor manera posible.

Si vemos cómo quedaría nuestra línea original con estos nuevos datos, tenemos lo siguiente:

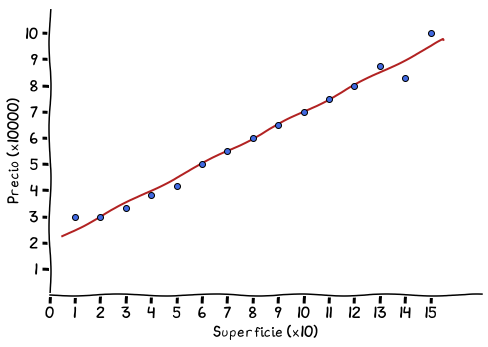Función lineal que establece precios de una casa dada su superficie, estimada a partir de los 15 datos

Cómo se puede observar, en este último gráfico, la línea no recorre todos los puntos tan de cerca como en el gráfico anterior, pero si se aproxima a la mayoría de ellos y no está tan lejos de aquellos puntos que están más lejos. Es algo mucho más sencillo de calcular y provee una solución suficientemente buena como para considerarla válida. El modelo no es perfecto, pero es lo suficientemente simple y general como para obtener resultados aproximadamente buenos y no sufre lo mismo que el caso de la curva anterior, donde al final crece sin control.

La verdadera forma de calcular la línea roja en este último caso no es tan sencilla como tomar dos puntos y calcular una pendiente y una intersección en el eje y. Se deben considerar todos los puntos para estimarla mejor. Sin embargo, el resultado al que se llega es bastante similar (el cambio se ve en los valores decimales) y la idea que está detrás del algoritmo que calcula esa línea, que se conoce como regresión lineal, es a grandes rasgos la misma que utilicé para calcular la línea a partir de los dos puntos originales.

Este es un ejemplo de regresión, algo que no es exclusivo del aprendizaje automático o incluso de la computación o la matemática. Es algo bastante común en ciencias económicas por ejemplo, donde se usa para predecir los valores del mercado.

Una aproximación sencilla a la clasificación

Parecido al caso anterior, la idea es encontrar una función que aproxime los datos. La diferencia fundamental está en que acá en lugar de encontrar una línea que pase por todos los puntos se busca encontrar algo que pueda diferenciar entre las clases del problema. Veamos un ejemplo:

Datos para clasificación

Así como están, los puntos no significan nada. Supongamos que en el eje x tenemos la cantidad de veces que hicimos click para ver un producto en Mercado Libre; por otro lado en el eje y tenemos la cantidad de preguntas que le hicimos al vendedor de ese producto; finalmente, cada punto representará si hicimos en verde si compramos el producto, y en rojo si no lo compramos. A partir de estos datos podemos construir el siguiente gráfico:

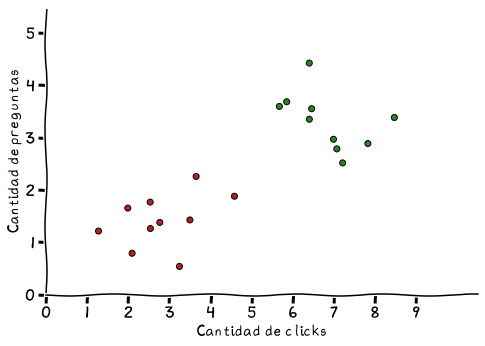Cantidad de clicks hechos sobre un producto (eje x) y cantidad de preguntas hechas al vendedor (eje y)

Esto es un ejemplo súper simplificado. Claramente no se reduce a entrar a ver un objeto o realizar preguntas sobre el mismo lo que nos hace comprar algo, aunque suelen ser buenos indicadores. No obstante, es útil como para entender el concepto de lo que hace un modelo de clasificación.

Como dije anteriormente, la clasificación trata de encontrar una función que permita diferenciar entre ambos grupos de puntos. ¿Cuál es esa función? Cómo es el caso del ejemplo de regresión, cualquier cosa que distinga a un grupo del otro sirve, pero si vamos al caso, estos son dos conjuntos linealmente separables, es decir que pueden diferenciarse por una función lineal.

La manera de calcular la función no es tan directa como tomar un par de puntos y calcular una pendiente y una intersección. Es algo más complejo que excede a lo que busco demostrar aquí. Sin embargo, una vez calculada, la función que servirá para clasificar es la que está representada por la línea celeste en el siguiente gráfico:

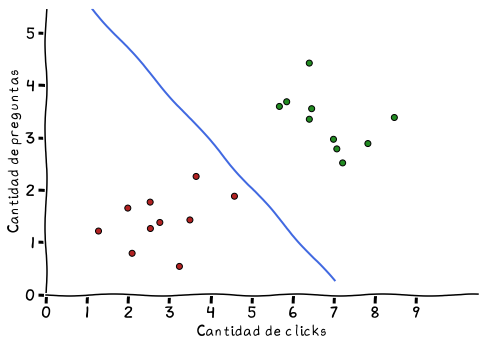Cantidad de clicks hechos sobre un producto (eje x) y cantidad de preguntas hechas al vendedor (eje y). La función representada en la línea celeste es el modelo de clasificación.

Con este modelo de clasificación, representado por la línea diagonal celeste, podemos tomar un par de características, cantidad de clicks y cantidad de preguntas hechas sobre un producto, y utilizar eso para ver donde cae el punto final en el gráfico. Si es arriba y a la derecha de la línea, entonces se puede pensar que hay intención de compra, y promocionar el producto; mientras que si el punto cae abajo y a la izquierda de dicha línea, la intención de compra es poca por lo que no conviene promocionar dicho producto.

En esencia esto es lo que hacen los modelos de clasificación de cualquier tipo, establecen funciones, a veces sencillas como en el ejemplo, a veces mucho más complejas, pero que buscan separar los datos en grupos para así categorizarlos.

Consideraciones finales

- Oh, por Dios, ¿Por qué tendrían de estos? - ¿Cuál es su problema? - Los lanzaremos al sol. El momento en que las computadoras que controlan nuestro arsenal nuclear se vuelven conscientes. Fuente: https://xkcd.com/1626

Espero que este artículo les haya sido lo suficientemente sencillo como para seguirlo, intenté hacerlo lo más general posible, porque considero que es importante entender qué es lo que hay detrás de varios de los sistemas que están presentes en la tecnología que usamos hoy en día.

Más allá de todo lo explicado, es importante tener en cuenta que el aprendizaje del que se habla no es tal, sino que está definido bajo un espectro muy limitado. Las máquinas no aprenden sólo aproximan, mediante funciones matemáticas, que a su vez toman versiones simplificadas, llevadas a números, de entidades del mundo real.

Algunas cosas se aproximan mejor, otras peor, pero siempre son aproximaciones, nunca son una verdad absoluta. Y como todo aquello que es aproximado, puede fallar (y generalmente lo hace), por lo que depender de estos sistemas a la hora de tomar decisiones de cualquier tipo, implica un riesgo, pero sobre todo a la hora de tomar decisiones que sean críticas y puedan afectar vidas de personas (e.g. en sistemas de reconocimiento facial para vigilancia, o modelos generación de texto que sean sexistas, xenófobos, racistas, etc).

Porque quizás no ocurra como en la película War Games donde una máquina es capaz de desencadenar una guerra nuclear; ni tampoco, si las máquinas fueran conscientes, pasaría lo del cómic de más arriba, pero la verdad es que estos modelos existen y afectan directamente la vida de las personas que probablemente no tuvieron o pudieron decidir nada sobre dichos modelos.